极值问题中的Fibonacci序列
(*话说刷过不少blog后发现博主们都喜欢一些自己专业之外的小东西,毕竟自己专业的东西看起来要么太trival,要么就太难以向读者讲清楚了*)
极值问题中的区间分割法
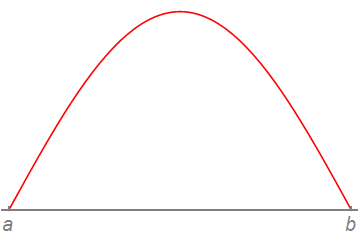
对于\([a,b]\)上的单峰函数,存在点\(x^* \in [a,b]\),使得函数在\([a,x^*]\)上单调递减,而在\([x^*,b]\)上单调递增。
-
\(f(x_1)>f(x_2)\)
根据引理,此时我们可以断定函数在区间段\([a,x_1]\)一定是单调增的。
那么极值点便在区间\([x_1,b]\)上,又可知函数在该区间上必然也是单峰函数,由此可以实现递归。 -
\(f(x_1)<f(x_2)\)
同样的分析,函数极值点在 区间\([a,x_2]\)上。 -
\(f(x_1)=f(x_2)\)
这个情况略有不同,极值点位于\([x_1,x_2]\)上。
好了,我们现在得到了一个略小的单峰区间。并且一般情况下,我们还知道这个区间内一个点的函数值。
那么下一步自然是在这个区间内再选取一个点,重复上面的步骤
现在问题来了,如何选取这些点?
黄金分割法
最简单的考量是希望每一步的迭代都是相似的,如图:
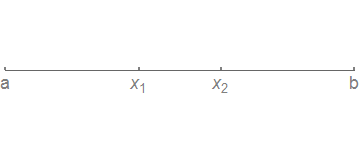
首先出于简单,我们令划分是对称的:\(x_1-a=b-x_2\)
然后不妨设下一个划分点位于\([a,x_2]\)上
我们期待\(x_1\)的函数值能够被复用,并且新问题与原问题有相似性,即
\[\tau=\frac{b-x_2}{b-a}=\frac{x_2-x_1}{x_2-a}\]
那么可以发现,我们可以加入一个新的分点\(x_3=x_2-\tau (x_2-a)\)来得到一个相似的结构,进而完成迭代
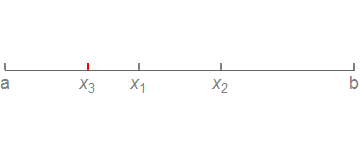
在这里,我们可以求得\(\tau=\frac{\sqrt{5}-1}{2}\approx 0.618\),正是黄金分割比。
这个方法我最初是在高中数学书的某本选修上看到的。另外,华罗庚在当年的政治大环境下,为了践行“理论指导实践”,曾大力推广这个方法。
Fibonacci方法
黄金分割法虽然简单易行,但却不一定是最优的选择。当然,我得首先给最优来一个清晰的定义:
计算选取\(k+1(k\ge 1)\)个点的函数值,在最坏的情况下,最后得到的单峰区间\(r_k^*\)最短。
我们尝试在这个意义下寻求最优的区间分割法。
首先考察\(k=1\)的情形,此时\(r_1^*=\max\{x_2-a,b-x_1\}\)
鉴于\(x_1<x_2\),可知当\(x_1=(a+b)/2-\varepsilon,x_2=(a+b)/2+\varepsilon\)时最优解可取得,其中\(\varepsilon\)为任意小的正实数,这时\(r_1^*=1/2\)
在下面的讨论中,为方便起见,将\([a,b]\)区间换做\([0,1]\)区间讨论
我们再重新审视一下整个过程:
- 为进行\(k\)阶的最优化,我们首先得给定第一个点\(\alpha\)(不妨设\(\alpha \ge 1/2\))、第二个点\(\beta \in (1-\alpha,\alpha)\)(这个选择容易证明是最优的)
- 然后选择一个区间,其长度为\(\alpha\)或者\(1-\beta\)
- 此后在这个区间中再取一个点
- 注意到此时该区间中已给定了一个点
-
如果如下问题的解被给出:
给定第一个点\(\alpha\),还能计算\(k\)个点的值,使得在最坏的情况下,最后得到的单峰区间\(r_k(\alpha)\)最短。 -
那么这个问题的\(k+1\)阶,即:
给定第一个点\(\alpha\),还能计算\(k+1\)个点的值,使得在最坏的情况下,最后得到的单峰区间\(r_{k+1}(\alpha)\)最短。
可以用上一个问题的解给出,从而得到递归表达式
为了方便起见,我们限定函数\(r_k(\alpha)\)的定义域为\([1/2,1]\)
那么有
\[r_{k+1}(\alpha)=\alpha \min r_{k}(\max\left\{\frac{\beta}{\alpha},1-\frac{\beta}{\alpha}\right\})\]
为了求解上述递归表达式,我们先考察较低阶的几个
\[r_1(\alpha)=\alpha\]
\begin{equation*}
\begin{aligned}
r_2(\alpha)&=\min\limits_{\beta \in (1-\alpha ,\alpha)}
\begin{cases}
\alpha~ r_1(\frac{\beta}{\alpha}) & \beta \ge \alpha/2 \\\\
\alpha~ r_1(1-\frac{\beta}{\alpha}) & \beta < \alpha/2
\end{cases}\\\\
&= \min\limits_{\beta \in (1-\alpha ,\alpha)}
\begin{cases}
\alpha & \beta \ge \alpha/2 \\\\
\beta-\alpha & \beta < \alpha/2
\end{cases}\\\\
&=\min\left\{
\max\{\alpha/2,1-\alpha\},\alpha/2~(when 1-\alpha<\alpha/2)
\right\}\\\\
&= \max\{\alpha/2,1-\alpha\}
\end{aligned}
\end{equation*}
上述的推导仅仅是寻找取值范围的上下界并带入的过程,注意始终记得下界要小于上界否则集合为空
根据结果,我们不妨做出猜测
\[
r_k(\alpha)=\max\left\{\frac{\alpha}{F_k},\frac{1-\alpha}{G_k}\right\}
\]
(*我知道这是有一点显得无耻,但是吗...总比原书上直接拿着结论来验证的好得多*)
那么有
\begin{equation*}
\begin{aligned}
r_{k+1}(\alpha) &= \min\limits_{\beta \in (1-\alpha, \alpha)}
\begin{cases}
\max\left\{\frac{\beta}{F_k},\frac{\alpha-\beta}{G_k}\right\}&\beta>\alpha/2 \\\\
\max\left\{\frac{\alpha-\beta}{f_k},\frac{\beta}{G_k}\right\}&\beta\le\alpha/2
\end{cases}\\\\
&=\min\limits_{\beta \in (1-\alpha, \alpha)}
\begin{cases}
\frac{\beta}{F_k} &\beta>\alpha/2\&\beta>\alpha\frac{F_k}{G_k+F_k} \\\\
\frac{\alpha-\beta}{G_k} &\beta>\alpha/2\&\beta\le\alpha\frac{F_k}{G_k+F_k} \\\\
\frac{\alpha-\beta}{F_k} &\beta\le\alpha/2\&\beta<\alpha\frac{G_k}{G_k+F_k} \\\\
\frac{\beta}{G_k} &\beta>\alpha/2\&\beta\ge\alpha\frac{G_k}{G_k+F_k}
\end{cases}\\\\
&=\min
\begin{cases}
\max\left\{\frac{\alpha}{G_k+F_k},\frac{\alpha}{2F_k},\frac{1-\alpha}{F_k}\right\} & \\\\
\frac{\alpha}{G_k+F_k} & \frac{\alpha F_k}{G_k+F_k}\ge\alpha/2~\&~\frac{\alpha F_k}{G_k+F_k}\ge1-\alpha \\\\
\max\left\{\frac{\alpha}{G_k+F_k},\frac{\alpha}{2F_k}\right\} & \alpha/2\ge1-\alpha~\&~\frac{\alpha G_k}{G_k+F_k}\ge1-\alpha \\\\
\max\left\{\frac{\alpha}{G_k+F_k},\frac{1-\alpha}{F_k}\right\} & \alpha/2\ge\frac{\alpha G_k}{G_k+F_k}~\&~\alpha/2\ge\frac{1-\alpha}{F_k}
\end{cases}\\\\
&=\min
\begin{cases}
\max\left\{\frac{\alpha}{G_k+F_k},\frac{\alpha}{2F_k},\frac{1-\alpha}{F_k}\right\} & \\\\
\max\left\{\frac{\alpha}{G_k+F_k},\frac{1-\alpha}{F_k}\right\} & \alpha/2>\frac{\alpha G_k}{G_k+F_k}~\&~\frac{1-\alpha}{F_k}
\end{cases}\\\\
&=\max\left\{\frac{\alpha}{G_k+F_k},\frac{1-\alpha}{F_k}\right\}
\end{aligned}
\end{equation*}
\begin{aligned}
F_{k+1}&=G_k+F_k\\\\
G_{k+1}&=F_k\\\\
F_1&=1\\\\
G_1&=1
\end{aligned}
\end{equation*}
\begin{aligned}
F_{k+1}=F_{k}+F_{k-1}\\\\
F_1=F_0=1
\end{aligned}
\end{equation*}
至此,最优的区间分割算法算是找到了。
叙述一下操作步骤:
为方便起见,考虑在区间\([0,F_k+1]\)上的极值问题:
- 取分点\(F_k,F_{k-1}\)
- 判断新的单峰区间。由对称性,我们只讨论落在\([0,F_k]\)上的情形
- 取分点\(F_{k-2}\)
- ......
- 取分点\(F_1=1\)后,再取分点\(F_0=1+\varepsilon\),由此可得到一个长度为一的单峰区间

讨论
由于Fibonacci数列相邻两项之比\(F_{k+1}/F_{k}\)当\(k\)趋向无穷时会趋向于黄金分割比\(\tau=\frac{1+\sqrt{5}}{2}\),我们惊奇的发现当\(k\)足够大时,这个算法趋向于,我们单纯从简单考虑所构造的,黄金分割算法。
考虑到Fibonacci数列的通项公式
\[
F(k)=[\tau^{k+1}-(-\tau)^{-k-1}]/\sqrt{5}
\]
容易证明
\[
\tau^{k+1}\ge F_{k+1}\ge\tau^k
\]
即\(k+1\)阶黄金分割法优于\(k\)阶Fibonacci法优于\(k\)阶黄金分割法
也就是说我们费尽心思找到的最优解法只省了一次不到的计算步长(╯‵□′)╯︵┻━┻
当然数学上的确蛮漂亮的。
再者现在做一维搜索,就算不能算导数,也一般会用二次插值之类的超线性收敛算法吧,谁还用这种破线性收敛算法
除非那个破函数真长这样_(:зゝ∠)_

(*其实我就是看书看不进没事干才来写这个东西耗时间的*)
