今天做计算概论的作业的时候出现了这样一道题：

有一组元素和一个空栈，给定元素入栈的顺序，问元素出栈的顺序有多少种(即出栈和入栈可以混合进行)

原题给的元素数量是4，枚举就可以了，但是很自然的就会想到n的情况该怎么做。

暴力点，首先就是写递推公式。定义\(G_m^n\)为栈内有m个元素，栈外有\(n-m\)个元素未进栈时，元素出栈的顺序的种数。很容易得到递推公式
\[
\begin{array}
lG_m^n &=& G_{m - 1}^n + G_{m + 1}^n\\
G_n^n &=& 1\\
G_{ - 1}^n &=& 0
\end{array}
\]

接下来...无路可走，不如丢Mma里算一算

F[m_, n_] := F[m, n] = Which[
    n == 0, 1,
    m < 0, 0,
    True, F[m - 1, n] + F[m + 1, n - 1]];

注意，这里在定义递归函数时多加了一项"F[m,n]"，这样可以将每一次计算出来的函数值存储起来，如果在递归调用的过程中遇见了曾经计算过的函数值的话，就能够调用曾经计算过的值而不是做重复的操作。这是属于用空间换时间的一个做法。考虑到这个具体问题，由于空间规模最大也就是\(O(n^2)\)的样子，而若不这样做时间规模可能高达\(O(2^n)\)，所以说这样做还是挺划算的。

这是计算结果

In[2]:= Table[F[0, n], {n, 0, 30}]

Out[2]={1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012,
742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190,
6564120420, 24466267020, 91482563640, 343059613650, 1289904147324,
4861946401452, 18367353072152, 69533550916004, 263747951750360, 
1002242216651368, 3814986502092304}

看上去挺像指数增长的，那么让我们取个对数吧

ListLinePlot[Log[%], PlotRange -> {0, Log[%[[-1]]]}]

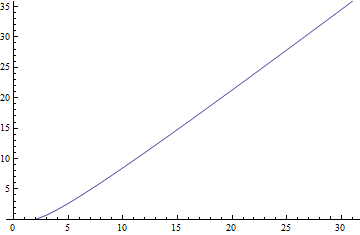
嗯...猜对了。但具体是什么呢...

正当我在做各种拟合的时候，叶神突然告诉我不要想了(之前问了他)，搞不出来的，这是一个叫卡特兰数的特殊数列，人家早就特别研究过了，你问wikipedia去吧。

然后我就很沮丧的去问了wikipedia(随便找个问题研究就有人弄过啊啊啊，而且还是弄不出来的啊啊啊)，然后更沮丧了——居然有这么简单的表达式！

\[Catalen_n=\frac{1}{n+1}C_{2n}^{n}\]

有了答案还是先不看过程了，先想想看。入栈和出栈操作需各执行n次，如果不考虑空栈不能出栈的要求的话，那么共有\(C_{2n}^{n}\)种排列方式。而考虑到这个要求的话是为什么要除以n+1呢？让我来想想。

......

......

......

还是看答案好了...

页面往下翻看到了四五种证明，随手挑了一个看着顺眼的证明看过去，看了大概五分钟，然后惊呆了。

证明梗概如下：

问题等价于有A元素与B元素各n个，对其进行一个排列，要求从任意位置向前看A元素的数目不大于B元素的数目，问满足条件的全体排列的总数。

记不满足此要求的全体排列构成的集合为\(K, \forall \alpha \in K\)，总可以找到一个位置，其前方元素A的个数等于元素B的个数加一，从而其后方元素A的个数等于元素B的个数减一。将后方元素中的A换做B, B换做A, 即得到一个由n+1个A与n-1个B构成的排列。记全体由n+1个A与n-1个B构成的排列组成的集合为\(F\)。则易知\(\forall \alpha \in K\), 都可如上映射到一个 \(\beta \in F\), 且\(\forall \beta \in F\), 都可以用同一个办法映射到一个\(\alpha \in K\), 即该映射是一一的，两集合元素个数相同，皆为\(C_{2n}^{n-1}\)。那么，满足题述条件的全体排列的总数为

\[C_{2n}^{n}-C_{2n}^{n-1}=\frac{1}{n+1}C_{2n}^{n}\]

命题得证。

这个方法被称为André's reflection method.

据wiki称这这数字不仅仅在这个地方有用，在不少排列组合的问题中都经常出现。比如说一个\(n*n\)的网格状街道，从右下角出发走到左上角，不允许穿过对角线，问有多少种不同的走法。上面的那个相对抽象的映射可以借助这个模型给出一个较为直观的说明：

即\(n*n\)的街道上禁止路径与\((n-1)*(n+1)\)的街道上全体路径的映射。

除此之外，这个数字还能表示：

• 节点数为n的全体不同构二叉树的数目
• 通过连接节点将n+2边的凸多边形划分成三角形的方案书
• 在圆上选择2n个点，将这些点成对连接起来使得所得到的n条线段不相交的方法数
• ......

处理时，可能需要用到另外一个递推关系：

\[{C_{n + 1}} = \sum\limits_{i = 0}^n {{C_i}{C_{n - i}}} \]

另外利用斯特令公式，容易得到科特兰数的渐进表达式

\[{C_n}{\rm{\~}}\frac{{{4^n}}}{{{n^{3/2}}\sqrt \pi  }}\]

第一阶为指数项，与之前数值模拟的结果相符。